How to change the notation and precision displayed by the online scientific calculator
The latest release of the online scientific calculator includes a new functionality: The preferences window. Here you can set the display format for the calculator results. This article gives a bit more information on how the calculator stores numbers internally, it’s precision limitations and explains how to use this new feature.
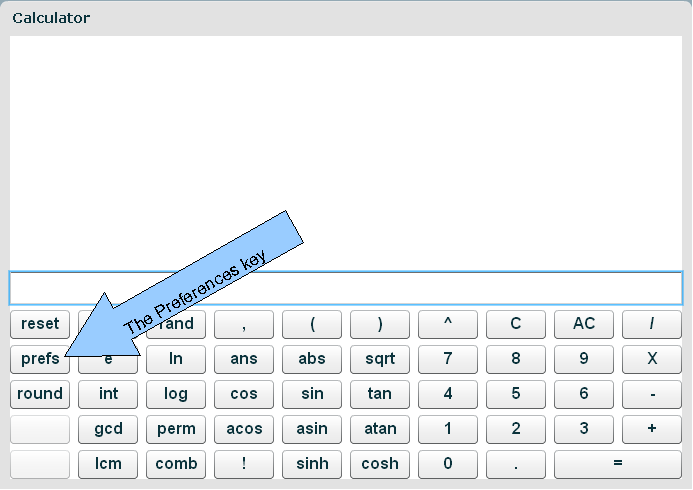
The prefs key
The preferences of the scientific calculator can be displayed and changed by pressing the prefs key:
A small dialog opens. It shows the current display preferences for the results. If you are accessing this feature for the first time, the values displayed and currently in use are the calculator’s default values: rounding decimals=9, notation=float. When you change the options from this window, the new values are saved for the next time you use the calculator from the same computer, regardless of which browser you use.
Your changes will be saved when you press ‘Apply’ or “OK’. The ‘Apply’ button applies the changes without closing the window. The ‘OK’ button applies the changes and also closes the window. Pressing the ‘Cancel’ button reverts to the previous values and closes the preferences dialog.
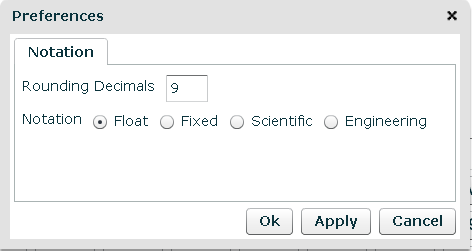
The Calculator Preferences Window
The preferences window contains two parameters, the ‘rounding decimals‘ field, where you can specify any number between 0 and 16, and the notation option that you can set to ‘float‘, ‘fixed‘, ‘scientific‘ or ‘engineering‘.
The Rounding Decimals field
Here you specify the maximum number of digits to display after the decimal point. The result is rounded.
It’s important to know that regardless of your display preferences, the calculator stores it’s results internally always maintaining the maximum possible precision. Here you can only change the way the results are displayed to you.
As an example, consider the result of the square root of 2:
If rounding decimals is 9 (and the notation is set to float) the result of sqrt(2) is displayed as 1.414213562, with 9 digits after the floating point
If rounding decimals is 6, the result displayed is 1.414214, only 6 figures after the decimal point. Note the rounding of the number.
If you are only interested in the integer portion, you can set the number of digits after the decimal point to 0, which will display the result as 1. As mentioned above, the value stored internally doesn’t change, it’s only the way the value is displayed ot you that changes. Take a look at the picture below:
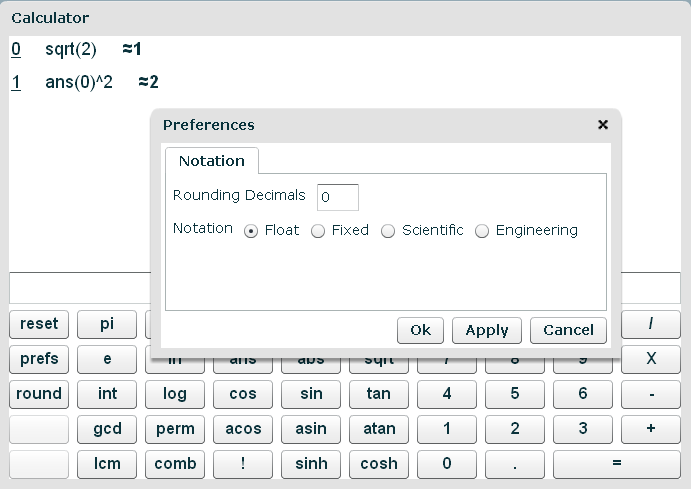
The Notation Parameter
The notation setting allows you to specify the format of the result and can be set to: ‘float‘ (the default), ‘fixed‘, ‘scientific‘ or ‘engineering‘.
Float tells the calculator to display all available digits up to the rounding decimals value described above. Example: if rounding decimals is 9, 3/4 is displayed as =0.75 .
Fixed tells the calculator to display a fixed number of digits after the decimal point. Example: if rounding decimals is 9, 3/4 is displayed as =0.750000000. The display includes 9 digits after the decimal point, even if they are all 0s.
Scientific causes the results to be displayed in scientific notation. Scientific notation is best used for numbers that are either very large or very small. Results are displayed as numbers with one digit before the decimal point multiplied by an appropriate power of 10. 3/4 =7.5*10^-1
Engineering is a special form of exponential notation, that only uses powers of 10 that are multiple of 3. Example: the number 12321 is displayed as 12.321*10^3 .
The calculator’s precision limitations
Playing around with the result display options, you will probably discover some of the precision limitations that are present in most calculators, online or otherwise:
Some of the results can be very surprising and are due to the bad habit of computers to store floating point numbers in binary format, a format that is incapable of representing certain real numbers. For example, try setting the decimal rounding to 16 and fixed notation, then calculate 0.1^-6. It should be 1000000, instead the result comes out to be 999999.9999999994179234 . These errors accumulate as the expressions get more complex, so remember to keep them into account if you care about the final accuracy of your calculations.
Tags: calculator precision, calculator preferences, Calculators, engineering notation, exponential notation, fixed notation, float, Howto, Integer, New Features, Online Calculator, Online Calculators, Online Scientific Calculator, precision, scientific notation